Fine-Gray检验与竞争风险模型

本文主要介绍生存资料处理的Fine-Gray检验与竞争风险模型，在生存资料处理中，这种方法目前应用越来越广泛。

1. 背景知识

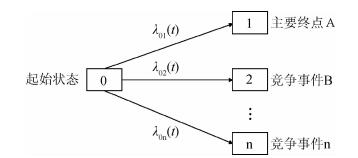
在观察某事件是否发生时，如果该事件被其他事件阻碍，即存在所谓“竞争风险”。研究中结局事件可能有多个，某些结局将阻止感兴趣事件的出现或影响其发生的概率，各结局事件形成“竞争”关系，互为竞争风险事件。

举例来说，某研究人员收集了本市2007年确诊为轻度认知损害（MCI）的518例老年患者临床资料，包括基本人口学特征、生活方式、体格检查和合并疾病信息等，并于2010~2013年完成6次随访调查，主要观察结局为发生阿尔兹海默病（AD）。随访期间，共发生AD78例，失访84例，其中28例搬迁、31例退出、25例死亡。试问影响MCI向AD转归的因素都有哪些？本例中，如果MCI患者在观察期间死于癌症、心血管疾病、车祸等原因而未发生AD，就不能为AD的发病做出贡献，即死亡“竞争”了AD的发生。传统生存资料统计方法将发生AD前死亡的个体、失访个体和未发生AD个体均按删失数据（censored data）处理，可能会导致估计偏差[1]。对于死亡率较高的老年人群，当有竞争风险事件存在时，采用传统生存分析方法（K-M法、Cox比例风险回归模型）会高估所研究疾病的发生风险，产生竞争风险偏倚，有人专门研究发现约46%的文献可能存在这种偏倚。

本例中若选用竞争风险模型处理较为恰当。所谓竞争风险模型（Competing Risk Model）是一种处理多种潜在结局生存数据的分析方法，早在1999年Fine和Gray就提出了部分分布的半参数比例风险模型，通常使用的终点指标是累积发生率函数（Cumulative incidence function，CIF）[1-2]。本例中可以将发生AD前死亡作为AD的竞争风险事件，采用竞争风险模型进行统计分析。竞争风险的单因素分析常用来估计关心终点事件的发生率，多因素分析常用来探索预后影响因素及效应值。

2. 案例分析

2.1 [案例分析] 

本案例数据来自http://www.stat.unipg.it/luca/R/。有研究者探讨骨髓移植对比血液移植治疗白血病的疗效，结局事件定义为“复发”，某些患者移植后不幸因为移植不良反应死亡，那这些发生移植相关死亡的患者就无法观察到“复发”的终点，也就是说“移植相关死亡”与“复发”存在竞争风险。故采用竞争风险模型分析[3-4]。

首先从当前工作路径中导入数据文件’bmtcrr.csv’。

library(foreign)
bmt <-read.csv('bmtcrr.csv')
str(bmt)

## 'data.frame':    177 obs. of  7 variables:
##  $ Sex   : Factor w/ 2 levels "F","M": 2 1 2 1 1 2 2 1 2 1 ...
##  $ D     : Factor w/ 2 levels "ALL","AML": 1 2 1 1 1 1 1 1 1 1 ...
##  $ Phase : Factor w/ 4 levels "CR1","CR2","CR3",..: 4 2 3 2 2 4 1 1 1 4 ...
##  $ Age   : int  48 23 7 26 36 17 7 17 26 8 ...
##  $ Status: int  2 1 0 2 2 2 0 2 0 1 ...
##  $ Source: Factor w/ 2 levels "BM+PB","PB": 1 1 1 1 1 1 1 1 1 1 ...
##  $ ftime : num  0.67 9.5 131.77 24.03 1.47 ...

这是一个数据框结构的数据，含有7个变量，共177个观测。 

$ Sex : 因子变量，2个水平：“F”,“M”。 

$ D : 因子变量，2个水平：“ALL(急性淋巴细胞白血病)”,“AML(急性髓系细胞白血病)”。 

$ Phase : 因子变量，4个水平：“CR1”,“CR2”,“CR3”,“Relapse”。 

$ Age : 年龄。 

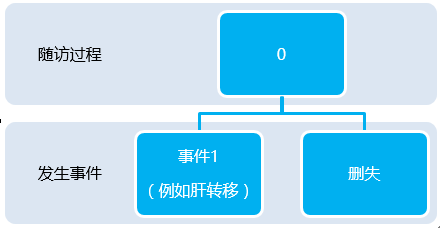
$ Status: 结局，0=删失，1=复发，2=竞争风险事件。 

$ Source: 因子变量，2个水平：“BM+PB(骨髓移植+血液移植)”,“PB(血液移植)”。 

$ ftime : 时间。

加载竞争风险模型的程辑包cmprsk，加载数据框bmt，并定义结局为因子变量。

library(cmprsk)

## Loading required package: survival

bmt$D <- as.factor(bmt$D)
attach(bmt)

2.2 Fine-Gray检验（单因素分析）

类比两组生存资料log-rank检验，考虑竞争风险事件，同样可以进行单因素分析与多因素分析。下面我们就可以使用cuminc()函数进行单因素的Fine-Gray检验。

fit1 <- cuminc(ftime,Status,D)
fit1

## Tests:
##        stat         pv df
## 1 2.8623325 0.09067592  1
## 2 0.4481279 0.50322531  1
## Estimates and Variances:
## $est
##              20        40        60        80       100       120
## ALL 1 0.3713851 0.3875571 0.3875571 0.3875571 0.3875571 0.3875571
## AML 1 0.2414530 0.2663827 0.2810390 0.2810390 0.2810390        NA
## ALL 2 0.3698630 0.3860350 0.3860350 0.3860350 0.3860350 0.3860350
## AML 2 0.4439103 0.4551473 0.4551473 0.4551473 0.4551473        NA
##
## $var
##                20          40          60          80         100
## ALL 1 0.003307032 0.003405375 0.003405375 0.003405375 0.003405375
## AML 1 0.001801156 0.001995487 0.002130835 0.002130835 0.002130835
## ALL 2 0.003268852 0.003373130 0.003373130 0.003373130 0.003373130
## AML 2 0.002430406 0.002460425 0.002460425 0.002460425 0.002460425
##               120
## ALL 1 0.003405375
## AML 1          NA
## ALL 2 0.003373130
## AML 2          NA

结果解读：

第一行统计量=2.8623325, P=0.09067592,表示在控制了竞争风险事件（即第二行计算的统计量和P值）后，“ALL”和“AML”累计复发风险无统计学差异P=0.09067592。

$est表示估计的各时间点“ALL”和“AML”组的累计复发率与与累计竞争风险事件发生率（分别用1和2来区分，与第一行第二行一致）。

$var表示估计的各时间点“ALL”和“AML”组的累计复发率与与累计竞争风险事件发生率的方差（分别用1和2来区分，与第一行第二行一致）。

下面我们画出累计复发率与累计竞争风险事件发生率的生存曲线，直观表示上述数字化结果。

plot(fit1,xlab = 'Month', ylab = 'CIF',lwd=2,lty=1,
     col = c('red','blue','black','forestgreen'))

图形解读：

纵坐标表示累计发生率CIF，横坐标是时间轴。我们从ALL1对应的红色曲线和AML1对应的蓝色曲线可以得出，ALL组的复发风险较AML 组高，但未达到统计学意义，P=0.09067592。同理，ALL2对应的黑色曲线在AML2对应的草绿色曲线下方，我们可以得出，ALL组的竞争风险事件发生率较AML组低，同样未达到统计学意义，P=0.50322531。从曲线上不难看出，在前20个月内，各条曲线“纠缠”在一起，所以并未得到有统计学意义的结果。简单来讲，这个图可以用一句话来概括：在控制了竞争风险事件后，“ALL”和“AML”累计复发风险无统计学差异P=0.09067592。

2.3 竞争风险模型（多因素分析）

下面我们进行考虑竞争风险事件的生存资料的多因素分析方法。在cmprsk包中，crr()函数可以很方便的实现多因素分析。该函数的用法如下：

crr(ftime, fstatus, cov1, cov2, tf, cengroup, failcode=1, cencode=0, subset, na.action=na.omit, gtol=1e-06, maxiter=10, init, variance=TRUE)

各参数具体解释各位可以参考crr()函数的帮助文档。此处需要说明的是，该函数必须指定时间变量与结局变量，然后传入协变量矩阵或数据框。首先定义进入模型的协变量，并定位为数据框的形式。

cov <- data.frame(age = bmt$Age,
                   sex_F = ifelse(bmt$Sex=='F',1,0),
                   dis_AML = ifelse(bmt$D=='AML',1,0),
                   phase_cr1 = ifelse(bmt$Phase=='CR1',1,0),
                   phase_cr2 = ifelse(bmt$Phase=='CR2',1,0),
                   phase_cr3 = ifelse(bmt$Phase=='CR3',1,0),
                   source_PB = ifelse(bmt$Source=='PB',1,0)) ## 设置哑变量
#cov

构建多因素的竞争风险模型。此处需要指定failcode=1, cencode=0, 分别代表结局事件赋值1与截尾赋值0，其他赋值默认为竞争风险事件2。

fit2 <- crr(bmt$ftime, bmt$Status, cov, failcode=1, cencode=0)
summary(fit2)

## Competing Risks Regression
##
## Call:
## crr(ftime = bmt$ftime, fstatus = bmt$Status, cov1 = cov, failcode = 1,
##     cencode = 0)
##
##              coef exp(coef) se(coef)      z p-value
## age       -0.0185     0.982   0.0119 -1.554  0.1200
## sex_F     -0.0352     0.965   0.2900 -0.122  0.9000
## dis_AML   -0.4723     0.624   0.3054 -1.547  0.1200
## phase_cr1 -1.1018     0.332   0.3764 -2.927  0.0034
## phase_cr2 -1.0200     0.361   0.3558 -2.867  0.0041
## phase_cr3 -0.7314     0.481   0.5766 -1.268  0.2000
## source_PB  0.9211     2.512   0.5530  1.666  0.0960
##
##           exp(coef) exp(-coef)  2.5% 97.5%
## age           0.982      1.019 0.959 1.005
## sex_F         0.965      1.036 0.547 1.704
## dis_AML       0.624      1.604 0.343 1.134
## phase_cr1     0.332      3.009 0.159 0.695
## phase_cr2     0.361      2.773 0.180 0.724
## phase_cr3     0.481      2.078 0.155 1.490
## source_PB     2.512      0.398 0.850 7.426
##
## Num. cases = 177
## Pseudo Log-likelihood = -267
## Pseudo likelihood ratio test = 24.4  on 7 df,

结果解读：在控制了竞争分险事件后，phase变量，即疾病所处阶段是患者复发的独立影响因素。以relapse阶段的患者为参照，CR1, CR2, CR3的累计复发分险较Relapse阶段的患者，HR及95% CI分别为0.332(0.159,0.695), 0.361(0.180,0.724), 0.481(0.155 1.490), 对应的P值分别为0.0034, 0.0041, 0.2000。

3. 讨论和总结

本文详细介绍了使用R的cmprsk程辑包进项Fine-Gray检验与竞争风险模型。笔者认为读者在具体应用过程中要注意两点：

第一，有选择性的使用Fine-Gray检验与竞争风险模型，如果终点事件存在竞争风险事件，而且极有可能对结论产生影响，那采用这个模型才是合适的，这个模型并非一定比Cox模型更优，这两个模型应该互为补充；

第二，竞争风险考虑的竞争风险事件也是有限的，目前仅是把Cox模型的二分类终点扩展为三分类，即结局事件，删失和竞争风险事件，即便如此，结果解读也变得很困难。读者在方法选择的时候应该做出更充分的评估和尝试。

4. 参考文献

[1].Fine JP and Gray RJ (1999) A proportional hazards model for the subdistribution of a competing risk. JASA 94:496-509. 

[2].Gray RJ (1988) A class of K-sample tests for comparing the cumulative incidence of a competing risk, ANNALS OF STATISTICS, 16:1141-1154. 

[3].Scrucca L., Santucci A., Aversa F. (2007) Competing risks analysis using R: an easy guide for clinicians. Bone Marrow Transplantation, 40, 381-387. 

[4].Scrucca L., Santucci A., Aversa F. (2010) Regression modeling of competing risk using R: an in depth guide for clinicians. Bone Marrow Transplantation, 45, 1388–1395.