贝叶斯统计中的一些基本的概念和方法介绍

1、分布函数（Distribution Function）

分布函数是指随机变量小于某个值的函数，即$F(x)=P(X<x)$，它和累积密度函数（Cumulative Density Function）是同一个意思。对于连续型分布来说，分布函数或者累积密度函数是概率密度函数（Probability Density Function）的积分：F(x)=\int_{-\infty}^{\infty} f(x) dxF(x)=∫​−∞​∞​​f(x)dx。对离散型分布来说，分布函数或者累积密度函数是一个阶梯状的分段函数。

2、概率密度函数（Probability Density Function）

仅针对连续型变量定义，可以理解成连续型随机变量的似然函数。它是连续型随机变量的分布函数的一阶导数，即变化率。如一元高斯分布的密度函数为：

f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{-2\sigma^2}}f(x)=​√​2π​​​σ​​1​​e​−​−2σ​2​​​​(x−μ)​2​​​​​​

3、概率质量函数（Probability Mass Function）

仅针对离散型随机变量定义，它是离散型随机变量在各个特定值上取值的概率。注意，连续型随机变量的概率密度函数虽然与离散型随机变量的概率质量函数对应，但是前者并不是概率，前者需要在某个区间进行积分后表示概率，而后者是特定值概率。连续型随机变量没有在某一点的概率的说法（因为每一点的概率密度函数都是0）。假设X是抛均匀硬币的结果，反面取值为0，正面取值为1。那么其概率质量函数为：

f(x) = \lbrace \begin{aligned} \frac{1}{2},\space x\in \{0,1\} \\ 0, \space x \notin \{0,1\} \end{aligned}f(x)={​​2​​1​​, x∈{0,1}​0, x∉{0,1}​​

4、似然函数（Likelihood Function）

简称似然，是指在某个参数下，关于数据的函数。它在统计推断问题中极其重要。一般表示为：

$\mathcal{L}(\theta |Y)=P(y|\theta )$

由于我们一般假设所有的数据都是独立同分布的，因此，似然的计算是所有数据的密度函数的乘积，这在计算中非常麻烦。所以我们一般使用Log-似然来计算。

5、边缘分布（Marginal Distribution）

在统计理论中，边缘分布指一组随机变量中，只包含其中部分变量的概率分布。例如随机变量$X$和$Y$，$X$的边缘分布是（离散型随机变量）：

P(x)=\sum_yP(x,y)=\sum_yP(x|y)p(y)P(x)=∑​y​​P(x,y)=∑​y​​P(x∣y)p(y)

连续型随机变量的边缘分布：

P(x) = \int_y p(x,y)dy=\int p(x|y)p(y)dyP(x)=∫​y​​p(x,y)dy=∫p(x∣y)p(y)dy

很多时候，统计的目标是做模型的参数估计。一般情况下，我们都有一堆已知的观测数据（观测结果，观测值）Y=\{y_1,y_2,\cdots,y_n\}Y={y​1​​,y​2​​,⋯,y​n​​}。通常，我们通过观察、根据理论等方式假设它是来自一个参数为$\theta$的某个分布，其参数未知，我们的目标就是估计这个参数的值（或者区间等）。同时，在贝叶斯推断中，还需要假设该分布的参数来自于另一个分布，称为先验分布，其参数为$\alpha$（很多时候，我们也是用参数表示该分布，比如用$\alpha$表示先验分布），它是我们在有观测值之前的一个主观判断，表明在有观测数据之前，你对这个分布或者数据的假设。另一个任务就是对新的观测值为\tilde{y}​y​~​​的预测，即计算预测分布。通常，我们会假设所有的数据都是相互独立，且来自相同的分布，即独立同分布假设（independent and identically distributed random variables, i.i.d.）

6、后验概率（Posterior Probability）

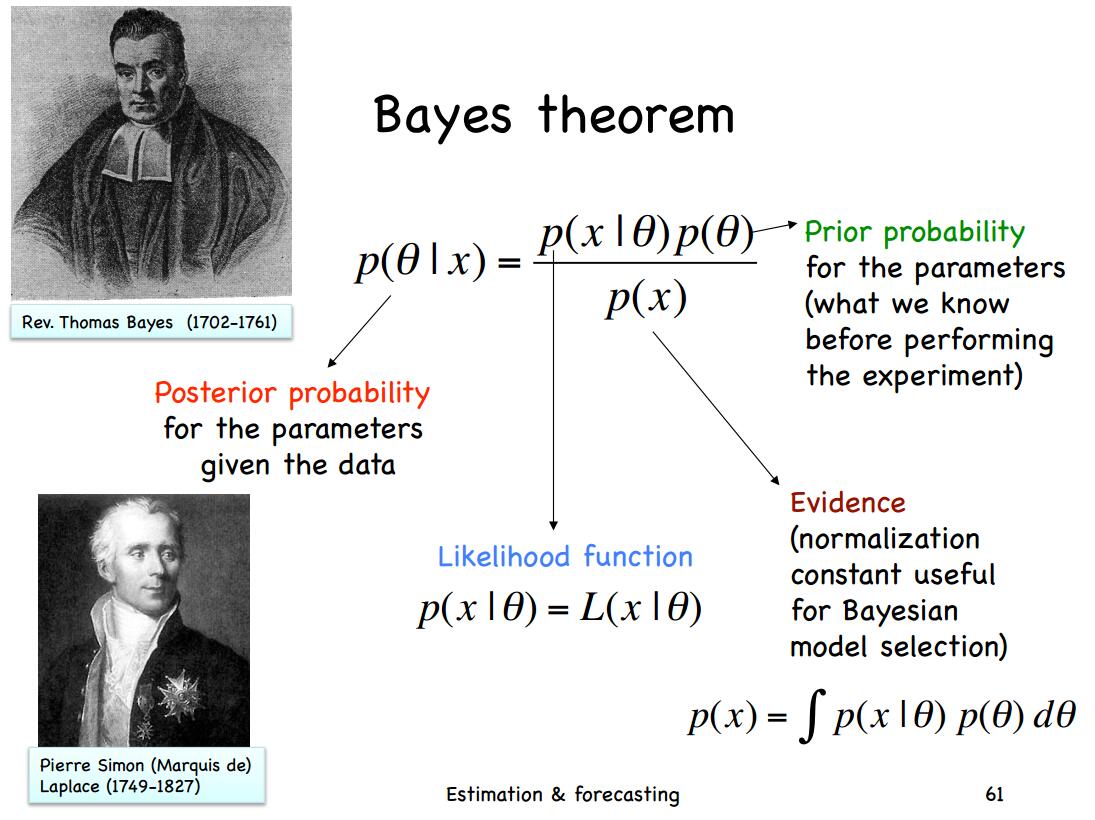
指某个随机事件，在某些证据（观测值）存在的条件下的概率。也就是指某个随机变量在有观测值条件下的概率，它是一个条件概率，即$p(\theta |Y)$，后验概率分布（Posterior Probability Distribution）（简称“后验”）就是这个变量的分布。根据贝叶斯公式，后验概率的计算如下：

p(\theta|Y) = \frac{p(Y|\theta)p(\theta)}{p(Y)} = c \times p(Y|\theta)p(\theta) \propto p(Y|\theta)p(\theta)p(θ∣Y)=​p(Y)​​p(Y∣θ)p(θ)​​=c×p(Y∣θ)p(θ)∝p(Y∣θ)p(θ)

由于观测值是已知量，因此分母是一个正规化数值，是一个常数。这里的$p(\theta )$就是一个先验分布的概率函数，是一个关于$\alpha$的函数。

7、先验概率（Prior Probability）

指某个随机变量的还没有出现观测值的时候人们判断其发生的概率。也就是人们对某个事件发生概率的主观判断。在贝叶斯中，先验概率与似然函数相乘可以得到后验概率。一般情况下，为了计算方便，我们都取共轭先验（Conjugate Prior），即当后验分布与先验分布属于同一种概率分布的时候，称该后验分布与先验分布为共轭分布。例如，在一元高斯分布中，当均值和方差均未知的时候，其先验分布是Noraml-Gamma分布。在这里，一般用$p(\theta |\alpha )$表示（或者直接将$\alpha$省略）。

8、预测分布（Predictive Distribution）

预测分布包括先验预测分布和后验预测分布。

8.1先验预测分布（Prior Predictive Distribution）

先验预测分布和后验预测分布很像，但是先验预测分布是在数据分布中将先验边缘化，在有观测值之前，未知参数$\theta$一般都可以使用先验分布表示$p(\theta )$，那么预测新数据就使用求$p(\theta )$的平均值的方式（注意，这里$p(\theta |\alpha )=p(\theta )$）：

p(\tilde{y}|\alpha) = \int p(\tilde{y}|\theta)p(\theta|\alpha)d\thetap(​y​~​​∣α)=∫p(​y​~​​∣θ)p(θ∣α)dθ

8.2、后验预测分布（Posterior Predictive Distribution）

指在有观测值情况下的未观测到的数据的分布，即p(\tilde{y}|Y)p(​y​~​​∣Y)。有了观测值之后，$\theta$的不确定性可以使用后验$p(\theta |Y)$更好地表示。因此，它不依赖于未知参数$\theta$，因为在有观测值的情况下，未知参数都会被积分掉。后验预测分布与后验分布的均值相同，但是方差更大（因为引入了新的数据），一般情况下，后验预测分布的作用比较大，可以用来估计模型参数等，先验预测用的较少，因为正常情况下我们都有一些观测数据：

p(\tilde{y}|Y) = \int p(\tilde{y}|\theta, Y)p(\theta|Y,\alpha)d\thetap(​y​~​​∣Y)=∫p(​y​~​​∣θ,Y)p(θ∣Y,α)dθ

9、贝叶斯计算的一般步骤

在使用贝叶斯做数据分析中，一般包括三个步骤：

1. 写出全概率的模型——将所有的观测值和未观测量放到一起，写出这个全概率的公式。
2. 写出基于观测数据的条件概率：计算合适的后验分布——在给定的观测数据下，写出我们感兴趣的变量的条件概率。
3. 评估模型的拟合情况和所得到的后验分布的含义——这个模型对数据的拟合程度怎么样，是否有合理的结论，步骤1中模型的假设是否具有敏感性？可以重复这三个步骤直到知道合适的模型。

10、（潜）隐变量模型（Latent Variable Models）

有很多复杂的后验分布都可以使用额外的参数（称为隐变量或者潜在变量）$z$使其变成一个可处理的形式。联合分布$p(\theta ,z|x)$首先被分解成潜在变量的边缘分布$p(z)$和一个条件分布$p(\theta |x,z)$的乘积形式。潜变量的边缘分布不依赖于观测数据，可以使用先验表示。这样扩展之后，那些可见参数$\theta$的分布可以通过边缘化获得：

$p(\theta |x)=\int p(\theta |x,z)p(z)dz$