列线图（Nomogram）原理，R实现方法

Nomogram 怎么用？

我们用个例子来说明Nomogram的用法，临床上用四个指标A,B,C,D来预测某疾病的发病率，其中A和B是连续性变量，C和D为二分类变量；A的取值范围在0-80之间，B的取值范围在0-10之间，C取值为Low和High，和D取值为Neg和Pos，在统计软件中建立回归模型，并绘制Nomogram，具体绘制出的图形如下：

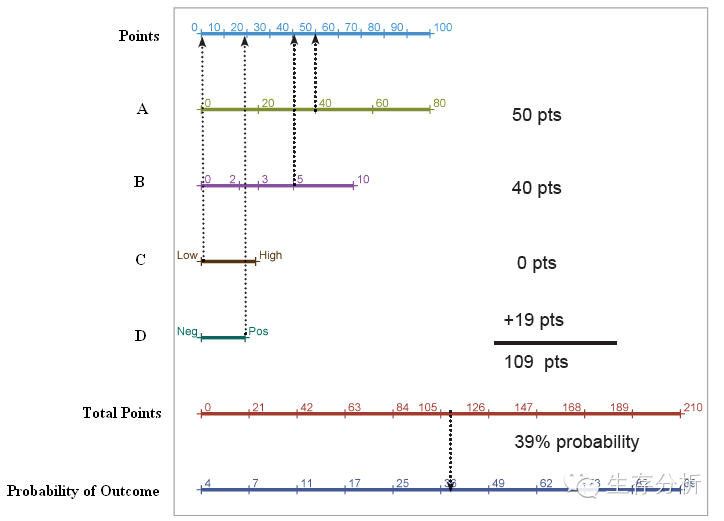
图1.Nomogram 示意图

假设有一个病人，他的四个因素的值分别是:A=40, B=5,C=Low和D=Pos，Nomogrm的用法是在A变量的刻度尺上找到其值为40的刻度，然后垂直画条竖线，对应到最上方的Points刻度尺上，找到Points对应的分值。我们看到图中A为40时，其Points是50，同理B=5时其Points是40，C=Low时其Points值是0，D=Pos时其Points值是19.将这四个因素的Points值加起来总共是109分;下一步在图下方的Total Points刻度尺上找到109，向下方的Probability of Clin.Outcome做垂线，109对应的值是39，则此病人该种疾病得发病风险预测概率值是39%。

Nomogram 绘制原理

一般的回归模型都可以绘制其对应的Nomogram，本文以二分类的Logistic 回归为例。例：为探讨某些危险因素对某种疾病的发病影响，统计建模筛选出的结果显示年龄（10-90），性别（男女）和血压（低，正常，高）是三个影响因素，利用这三个因素与二分类的结局变量做Logistic回归,回归结果见下表：

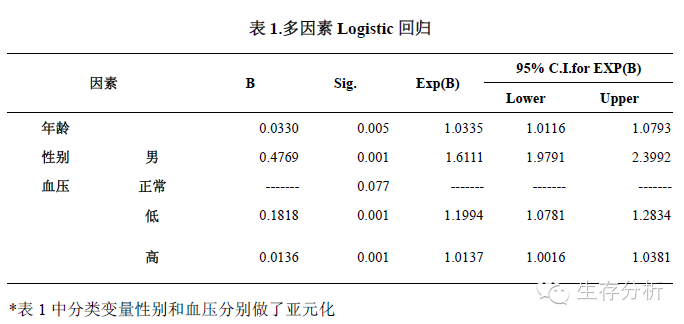
1. 对每个自变量（因素）赋分

一般情况下，绘制Nomogram时要求每个因素的赋分范围在0-100之间。Nomogram绘制实际上是对上述回归结果的系数做转化后以图形的形式展现出来，即主要是对回归模型拟合系数的转化。

（1）系数转换

对于连续性变量年龄，其范围是10-90，结合表1中估计的各因素的系数，Nomogram的转换公式是：

（2）根据转换结果赋分

绘制Nomogram的最核心点是哪个变量对预测结果影响最大，然后以影响最大的指标为基础（即Nomogram的第一条刻度线），第二影响大的指标以第一影响大的指标为基础，按照一定的公式转换成比例，第三影响大的指标同样以第一大的指标为基础，做一定的转换。换句话说，Nomogram的每个指标的标尺，是以影响最大的指标为参考做出来的。

本例中，按照转换的系数值大小排序及赋分结果见表2。

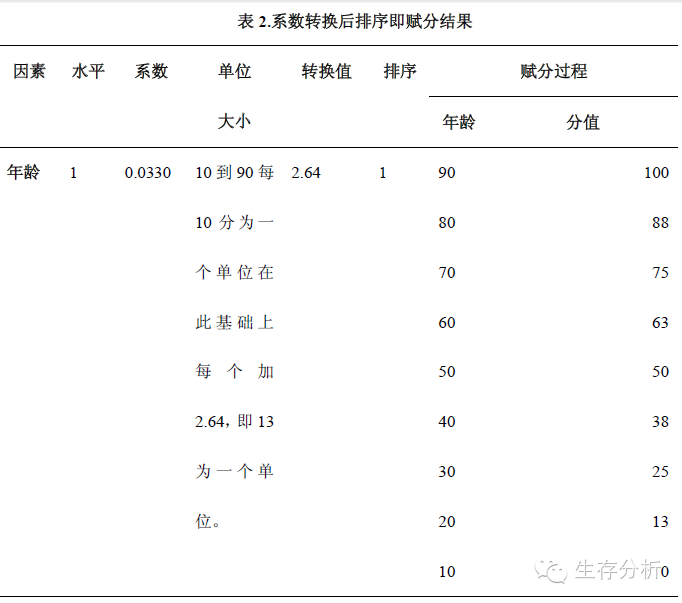
上面步骤即完成了最基本的每个因素的赋分过程，即每个因素刻度尺的确定及刻度尺所对应的Points的值。

Nomgram的R语言实现代码

简单的说这是一种将Logistic回归或Cox回归图形化呈现的方法，可以让读者从图中很简便地根据预测变量的值得到因变量的大致概率数值。其对于Logistic回归或Cox回归的意义，大概相当于散点图对于简单线性回归的意义。

下面简单说下Nomogram怎么看。如下图。欲知年龄50岁的女性（sex=1）的患病风险，只需要将age=45岁向points轴投射，则points=50；同理sex=1时，points≈37。两者相加则Total points=87；将此数值在Total points轴上向Risk概率轴投射，则可知风险大概在0.4和0.5之间。（参见图中红线）对于单个变量，只需要令Total points = points进行投射即可。

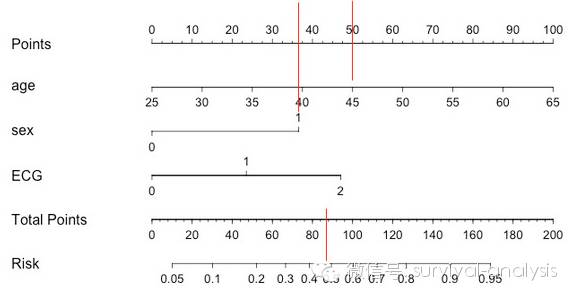
接下来讲如何用R语言做出上面的这张图。简单起见，此帖仅讨论Logistic回归，Cox回归的方法类似，但相对更复杂。

本帖所用数据引用自上海交大出版《医学统计学及SAS应用（修订版）》的例11.4

require(rms) ##调用rms包

# 建立数据集
y = c(0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1,
1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1,
1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0,
0, 0, 1, 0, 1, 0, 1, 0, 1)
age = c(28, 42, 46, 45, 34, 44, 48, 45, 38, 45, 49, 45, 41, 46, 49, 46, 44, 48,
52, 48, 45, 50, 53, 57, 46, 52, 54, 57, 47, 52, 55, 59, 50, 54, 57, 60,
51, 55, 46, 63, 51, 59, 48, 35, 53, 59, 57, 37, 55, 32, 60, 43, 59, 37,
30, 47, 60, 38, 34, 48, 32, 38, 36, 49, 33, 42, 38, 58, 35, 43, 39, 59,
39, 43, 42, 60, 40, 44)
sex = c(0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1,
0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1,
0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1,
0, 1, 1, 1, 0, 1)
ECG = c(0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1,
0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 2, 1, 0, 0, 2, 2, 0, 0, 2, 2,
0, 1, 2, 2, 0, 1, 0, 2, 0, 1, 0, 2, 1, 1, 0, 2, 1, 1, 0, 2, 1, 1, 0, 2,
1, 1, 0, 2, 1, 1)
# 设定nomogram的参数
ddist <- datadist(age, sex, ECG)
options(datadist='ddist')
# logistic回归
f <- lrm(y ~ age + sex + ECG)
# nomogram
nom <- nomogram(f, fun=plogis,
fun.at=c(.001, .01, .05, seq(.1,.9, by=.1), .95, .99, .999),
lp=F, funlabel="Risk")
plot(nom)

有朋友问到Cox回归的代码怎么写。Cox回归模型会复杂一些，因为可能涉及到不同时间点（3年、5年）生存概率的计算。下面讨论最简单的概率轴为中位生存时间的情况。

require(rms)
require(Hmisc) ##需要下载安装

require(survival) ##R默认自带的用于做生存分析的包
# 建立数据集（使用rms包example的代码，未改动）
n <- 1000
set.seed(731)
age <- 50 + 12*rnorm(n)
label(age) <- "Age"
sex <- factor(sample(c('Male','Female'), n,
rep=TRUE, prob=c(.6, .4)))
cens <- 15*runif(n)
h <- .02*exp(.04*(age-50)+.8*(sex=='Female'))
dt <- -log(runif(n))/h
label(dt) <- 'Follow-up Time'
e <- ifelse(dt <= cens,1,0)
dt <- pmin(dt, cens)
units(dt) <- "Year"
# 设定nomogram的参数
ddist <- datadist(age, sex)
options(datadist='ddist')
# Cox回归
S <- Surv(dt,e)
f <- cph(S ~ rcs(age,4) + sex, x=T, y=T)
med <- Quantile(f)
# nomogram
nom <- nomogram(f, fun=function(x) med(x),
fun.at=c(13,12,11,9,8,7,6,5),lp=F, funlabel="Median Survival Time")
plot(nom) ##绘制Nomgram图

以上是R语言实现Nomgram的程序

内容来自于生存分析微信号