用SPSS进行非线性回归分析实例

非线性回归分析

在回归分析中，当自变量和因变量间的关系不能简单地表示为线性方程，或者不能表示为可化为线性方程的时侯，可采用非线性估计来建立回归模型。

SPSS提供了非线性回归“Nonlinear”过程，下面就以实例来介绍非线性拟合“Nonlinear”过程的基本步骤和使用方法。

应用实例

研究了南美斑潜蝇幼虫在不同温度条件下的发育速率，得到试验数据如下：

表5-1 南美斑潜蝇幼虫在不同温度条件下的发育速率

根据以上数据拟合逻辑斯蒂模型：

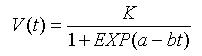
本例子数据保存在DATA6-4.SAV。

1）准备分析数据

在SPSS数据编辑窗口建立变量“t”和“v”两个变量，把表6-14中的数据分别输入“温度”和“发育速率”对应的变量中。

或者打开已经存在的数据文件（DATA6-4.SAV）。

2）启动线性回归过程

单击SPSS主菜单的“Analyze”下的“Regression”中“Nonlinear”项，将打开如图5-1所示的线回归对话窗口。

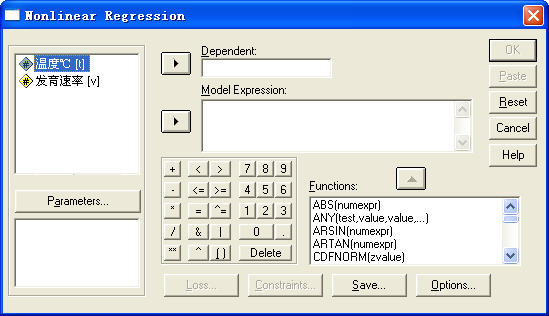
图5-1 Nonlinear非线性回归对话窗口

3) 设置分析变量

设置因变量：从左侧的变量列表框中选择一个因变量进入“Dependent(s)”框。本例子选“发育速率[v]”变量为因变量。

4) 设置参数变量和初始值

单击“Parameters”按钮，将打开如图6-14所示的对话框。该对话框用于设置参数的初始值。

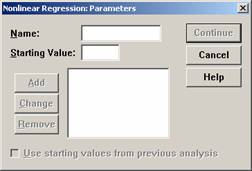
图5-2 设置参数初始值

“Name”框用于输入参数名称。

“Starting”框用于输入参数的初始值。

输入完参数名和初始值后，单击“Add”按钮，则定义的变量及其初始值将显示在下方的参数框中。需要修改已经定义的参数变量，先用将其选中，然后在“Name”和“Starting”栏里进行修改，完成后点击“Change”按钮确认修改。要删除已经定义的参数变量，先用将其选中，然后点击“Bemove”按钮删除。

在本例逻辑斯蒂模型中估计的参数有“K”、“a”和“b”三个参数变量。设置初始值为：K=0.1；a=3；b=0.1。

参数的初始值可根据给定模型中参数定义范围情况而定。输入后的“Nonlinear”对话窗口如下图。

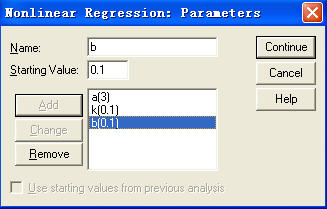
图5-3 设置参数初始值后的对话框

完成后点击“Continue”按钮。

5）输入方程式

在“Model Expression”框中输入需要拟合的方程式，在该方程中包含自变量、参数变量和常数等。自变量和参数变量可以从左边的列表框和“Parameters”框里选入。

方程中的函数可以从“Function”框里选入；运算符号和常数可以用鼠标从窗口“数字符号”显示区中点击输入。

本例输入的逻辑斯蒂模型是： K/(1+EXP(a-b*t))。输入后的窗口显示如下图。

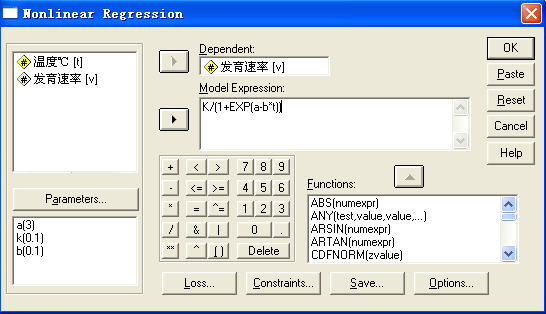
图5-4 设置后的非线性回归对话窗口

6) 迭代条件

在主对话框中单击“Loss”按钮，将打开如图5-5所示的对话框。

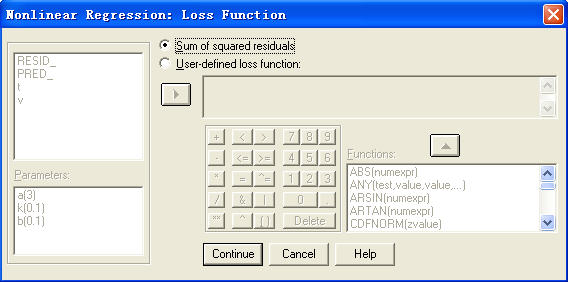
图5-5 Loss 对话框

        Sum of squared residuals”项，残差平方和最小值，系统默认。本例选该项。
        “User-defined loss function”自定义选项。设置其他统计量为迭代条件，在下边输入框中输入相应的统计
               量的表达式，称为损失函数。在左上角的变量列表框中，“RESID”代表所选变量的残差；“PRED_”代表预测
               值。可以从左下角框中选择已定义的参数进入损失函。

7）参数取值范围

在主对话框中单击“Constraints”按钮，将打开如图5-6所示的对话框。在该对话框中设置回归方程中参数的取值范围。

选中“Define parameter constraint”项，即可对选定的参数变量设置取值范围。参数的取值范围，用不等式“=,<=,>=”来定义。

例如，在本例逻辑斯蒂模型中K参数应该小于1。应该定义如下：k<=0.9999

定义后会提示：是否复制现有的变量名，回答“确定”。

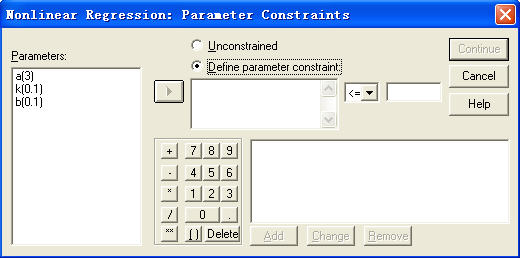
图5-6 参数取值范围对话框

8) 保存分析数据

在主对话框中单击“Save”按钮将打开如图5-7所示的对话框，选择要保存到数据文件中的统计量。

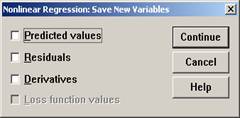
图 5-7 Save对话框

其中各项分别为：

       “Predicted values”因变量的预测值。
       “Residuals”因变量的残差。
       “Derivatives”派生数。
       “Loss function values”损失函数值。

9) 迭代方法

主对话框中单击“Options”按钮，将打开如图5-8所示的对话框。

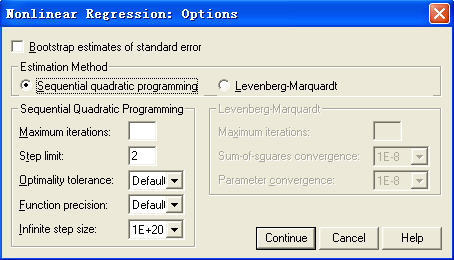
图5-8 迭代方法对话框

“Bootstrap estimates of standard error”项，将采用样本重复法计算标准误。样本重复法需要顺序二次规划算法的支持。当选中该项时，SPSS将自动选中“Sequential quadratic Programming”项。

“Estimation Method”框中列出了参数的两种估计方法：

“Sequential Quadratic Programming”项为顺序二次规划算法。该方法要求输入的参数为：



“Maximum”最大迭代步数。 “Step Iimit”最大步长。 “Optimality”目标函数的迭代误差限。 “Function”函数精度，应比目标函数的迭代误差限小。 “Infinite step”当一次迭代中参数值的变化大于设置值，则迭代停止。

“Levenberg-Marquardt”项，采用麦夸尔迭代法)，系统缺省设置。该法要求输入的参数为：

“Maximum iterations”最大迭代步数。 “Sum-of-squares convergence”在一步迭代中目标函数残差平方和的变化比例小于设置的值时，                         迭代停止。 “Parameter convergence”在一步迭代中参数的变化比例小于设置值时，迭代停止。

本例选“Levenberg-Marquardt”项，最大迭代步数100，残差平方和的变化比例小于1E-8，参数的变化比例小于1E-8。

 

10）提交执行

所有的设置完成后，在主对话框中点击“OK”按钮提交所有设置，SPSS执行过程后输出结果显示在输出窗口中。

11) 结果分析

结果:

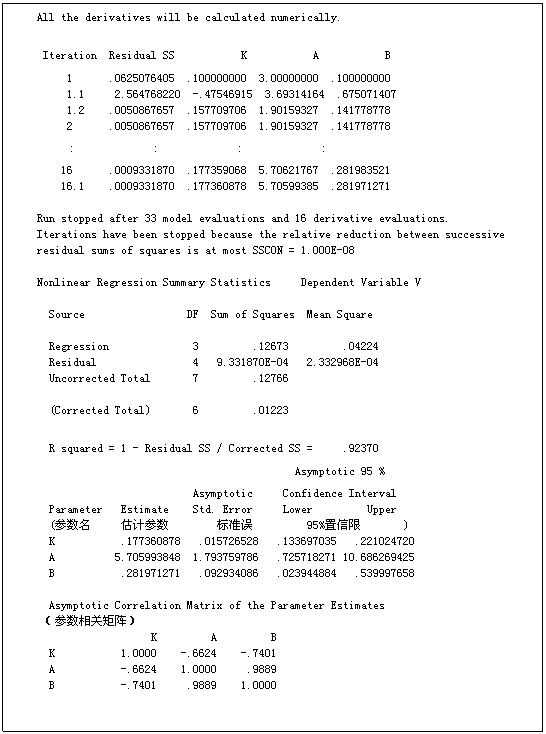
根据以上输出结果得到K的参数估计值是0.177360878；a的参数估计值是5.705993848；b的参数估计值是0.281971271。其拟合的逻辑斯蒂发育速率模型为：

残差平方和（Q）为0.0009331870；拟合优度系数（R2）为0.92370。