第十一章 Logistic回归分析命令与输出结果说明
2012-04-17 生物谷 生物谷
logistic 因变量 变量1 变量2… 变量m lfit clogit 因变量 变量1 变量2… 变量m,strata(配对编号变量) [or] 非 条 件 logistic 回 归 命 令 为 logistic,logistic 回 归 模 型 要 求 因 变 量 为 0-1 变 量。 即:
|
logistic 因变量 变量1 变量2… 变量m lfit clogit 因变量 变量1 变量2… 变量m,strata(配对编号变量) [or] |
非 条 件 logistic 回 归 命 令 为 logistic,logistic 回 归 模 型 要 求 因 变 量 为 0-1 变 量。 即: 要 求 结 果 为 两 种 情 况: 发 生( 因 变 量=1) 或 未 发 生( 因 变 量=0)。 结 果 为 发 生 的 模 型 表 达 式 为:
 以 及
以 及 
其 中 参 数 ![]() , 由 上 式 可 得:
, 由 上 式 可 得:
P(Y=0)=1-P(Y=1)
所 以 对 因 变 量 而 言,logistic 模 型 本 质 上 是 一 个 带 参 数 的 二 项 分 布 的 模 型, x1,x2,…,xm 为 协 变 量, 用 这 些 协 变 量 刻 划 研 究 问 题 中 的 各 种 情 况, 再 由 这 些 协 变 量 构 成 的 线 性 表 达 式 作 为 模 型 的 参 数 对 应 这 些 相 应 的 发 生 概 率 P(Y=1)。lfit 是 模 型 适 定 性 诊 断 命 令;clogit 是 条 件 logistic 回 归 命 令。
例: 为 了 分 析 研 究 一 组 病 患 者, 经 治 疗 后 的 病 情 恢 复 情 况。 设 变 量 Y 为 恢 复 状 况 (Y=0 表 示 未 恢 复,Y=1 表 示 恢 复), 变 量 x1 为 病 情 严 重 程 度 (x1=0 表 示 不 严 重,x1=1 表 示 严 重), 变 量 x2 为 年 龄( 岁), 变 量 x3 为 疗 法 (x3=0 表 示 新 疗 法,x3=1 表 示 传 统 疗 法)。 现 测 得 40 名 病 人 有 关 的 数 据 资 料 如 下, 试 作 非 条 件 logistic 回 归 分 析( 资 料 摘 自 医 用 多 元 统 计 分 析 教 材, 曹 素 华 主 编)。
|
编 号 |
Y |
x1 |
x2 |
x3 |
编 号 |
Y |
x1 |
x2 |
x3 |
|
1 |
1 |
0 |
20 |
1 |
21 |
0 |
0 |
34 |
1 |
|
2 |
1 |
0 |
23 |
1 |
22 |
0 |
0 |
30 |
1 |
|
3 |
1 |
0 |
32 |
1 |
23 |
0 |
0 |
38 |
1 |
|
4 |
1 |
0 |
38 |
1 |
24 |
0 |
0 |
37 |
1 |
|
5 |
1 |
1 |
25 |
1 |
25 |
0 |
1 |
24 |
1 |
|
6 |
1 |
0 |
20 |
0 |
26 |
0 |
1 |
25 |
1 |
|
7 |
1 |
0 |
24 |
0 |
27 |
0 |
1 |
29 |
1 |
|
8 |
1 |
0 |
28 |
0 |
28 |
0 |
1 |
32 |
1 |
|
9 |
1 |
0 |
30 |
0 |
29 |
0 |
1 |
34 |
1 |
|
10 |
1 |
0 |
32 |
0 |
30 |
0 |
1 |
37 |
1 |
|
11 |
1 |
0 |
38 |
0 |
31 |
0 |
1 |
40 |
1 |
|
12 |
1 |
1 |
26 |
0 |
32 |
0 |
1 |
40 |
1 |
|
13 |
1 |
1 |
29 |
0 |
33 |
0 |
0 |
33 |
0 |
|
14 |
1 |
1 |
34 |
0 |
34 |
0 |
0 |
36 |
0 |
|
15 |
1 |
1 |
33 |
0 |
35 |
0 |
1 |
24 |
0 |
|
16 |
1 |
1 |
38 |
0 |
36 |
0 |
1 |
34 |
0 |
|
17 |
1 |
1 |
40 |
0 |
37 |
0 |
1 |
32 |
0 |
|
18 |
0 |
0 |
22 |
1 |
38 |
0 |
1 |
36 |
0 |
|
19 |
0 |
0 |
26 |
1 |
39 |
0 |
1 |
38 |
0 |
|
20 |
0 |
0 |
29 |
1 |
40 |
0 |
0 |
39 |
0 |
在 本 例 中, 结 果 本 例 虽 然 不 是 死 亡 或 生 存 变 量, 当 与 此 对 应:Y=1 恢 复 对 应 死 亡;Y=0 未 恢 复 对 应 生 存( 即: 结 果 为 没 有 发 生 变 化)。
logistic y x1 x2 x3
|
Logit Estimates Number of obs = 40 ① chi2(3) = 9.53 ③ ② Prob > chi2 = 0.0230 Log Likelihood = -22.509701 ④ Pseudo R2 = 0.1747 -------------------------------------------------------------------------------------------- ⑤ ⑥ ⑦ ⑧ ⑨ y | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval] ---------+--------------------------------------------------------------------------------- x1 | .4599424 .3448279 -1.036 0.300 .1058135 1.999245 x2 | .8987332 .0608538 -1.577 0.115 .7870375 1.026281 x3 | .1412747 .1135345 -2.435 0.015 .0292417 .682538 -------------------------------------------------------------------------------------------- |
① 为 模 型 无 效 假 设( 即:所 有 协 变 量 的 比 数 比 为 1) 所 对 应 的 似 然 比 检 验( 其 自 由 度 为 协 变 量 个 数 的卡 方); ② 模 型 无 效 假 设 检 验 对 应 的 p 值;③ 对 数 似 然 比;④ 伪 决 定 系 数;⑤ 比 数 比;⑥ 比 数 比 的 标 准 误;⑦ 单 个 比 数 比 检 验 的Z 统 计 量;⑧ 单 个 比 数 比 检 验 的 p 值;⑨ 比 数 比 的 95% 可 信 限。
本 例 结 果 表 明: 通 过 平 衡 病 情 严 重 程 度 x1 和 年 龄 x2 的 混 杂 因 素 影 响, 传 统 疗 法(x3=1) 对 于 恢 复 和 未 恢 复 的 比 数(Odds) 显 著 地 小 于 新 疗 法(x3=0) 的 恢 复 和 未 恢 复 的 比 数(Odds) ( 比 数 比 OR=0.14127,p=0.015)。
· 条 件 logistic 回 归 模 型( 即: 配 对 logistic 模 型)
STATA 命 令:
clogit 因 变 量 变量1 变量2… 变量m,strata( 配对编号变量) [or]
因 变 量 为 二 值 变 量 Y (一 般 为 发 病 Y=1 和 不 发 病 Y=0, 也 可 以 其 它 类 似 情 况 与 其 对 应),变量1 变量2… 变量m 为 协 变 量。 在 配 对 1:1 的 条 件 下, 发 病 的 概 率 为:

其 中 ![]() 为 患 者 的 协 变 量,
为 患 者 的 协 变 量, ![]() 为 对 照 的 协 变 量,
为 对 照 的 协 变 量, ![]() 为 模 型 参 数, 即:要 有 数 据 对 模 型 拟 合 才 能 得 到 的 这 些 参 数 的 估 计 值。
为 模 型 参 数, 即:要 有 数 据 对 模 型 拟 合 才 能 得 到 的 这 些 参 数 的 估 计 值。
例: 为 了 研 究 胃 癌 的 危 险 因 素, 某 医 学 院 用 103 对 1:1 配 对 的 病 例 对 照 资 料, 对 胃 癌 发 病 概 率 和 七 个 因 素 的 关 系 进 行 条 件 logistic 回 归 分 析。 这 里 仅 选 其 中 10 对 三 个 因 素 资 料( 见 表), 试 作 胃 癌 发 病 概 率 和 这 三 个 因 素 的 条 件 logistic 回 归 分 析。
变 量 定 义(data coding)
|
变量名 |
因素 |
取值 |
|
x1 |
蛋白蛋类摄入量 |
0,1,2,3 |
|
x2 |
不良饮食习惯 |
0,1,2,3 |
|
x3 |
精神因素 |
0,1,2,3 |
|
id |
配 对 编 号 |
1---10 |
|
Y |
是 否 患 胃 癌 |
0: 对 照;1: 胃 癌 患 者 |
数 据:( 资 料 摘 自 医 用 多 元 统 计 分 析, 曹 素 华 主 编)
|
id |
y |
x1 |
x2 |
x3 |
id |
y |
x1 |
x2 |
x3 |
|
1 |
1 |
1 |
3 |
0 |
6 |
1 |
0 |
2 |
2 |
|
1 |
0 |
1 |
0 |
1 |
6 |
0 |
2 |
0 |
0 |
|
2 |
1 |
0 |
3 |
1 |
7 |
1 |
1 |
1 |
1 |
|
2 |
0 |
1 |
3 |
0 |
7 |
0 |
0 |
0 |
0 |
|
3 |
1 |
0 |
1 |
2 |
8 |
1 |
1 |
1 |
2 |
|
3 |
0 |
0 |
2 |
0 |
8 |
0 |
0 |
0 |
0 |
|
4 |
1 |
1 |
2 |
0 |
9 |
1 |
3 |
3 |
2 |
|
4 |
0 |
1 |
0 |
0 |
9 |
0 |
2 |
2 |
0 |
|
5 |
1 |
1 |
1 |
1 |
10 |
1 |
2 |
2 |
2 |
|
5 |
0 |
1 |
2 |
本文系梅斯医学(MedSci)原创编译整理,转载需授权!--> 小提示:本篇资讯需要登录阅读,点击跳转登录
版权声明:
本网站所有内容来源注明为“梅斯医学”或“MedSci原创”的文字、图片和音视频资料,版权均属于梅斯医学所有。非经授权,任何媒体、网站或个人不得转载,授权转载时须注明来源为“梅斯医学”。其它来源的文章系转载文章,或“梅斯号”自媒体发布的文章,仅系出于传递更多信息之目的,本站仅负责审核内容合规,其内容不代表本站立场,本站不负责内容的准确性和版权。如果存在侵权、或不希望被转载的媒体或个人可与我们联系,我们将立即进行删除处理。 在此留言 
相关资讯Stata第六章 卡方检验本节STATA 命令摘要 [by 分层变量名:]tab2变量1变量2[,allchi2exactcellcolumnrow] tabi#11#12[...]\[#21#22[...][\...][,allchi2exactcellcolumnrow] ·列联表分析 STATA命令: [by分层变量:]tab2变量1变量2[,allchi2lichi2e Stata第十章 线性回归和逐步回归命令和输出结果说明本节STATA命令摘要: regress 因变量 变量1变量2…变量m,beta stepwise 因变量 变量1变量2…变量m,ba forwstfe(#)fs(#) test表达式 predict 新变量 predict 新变量,resi Stata第七章 相关分析本节STATA 命令摘要 correlate变量名1变量名2…变量名m spearman变量1 变量2 · 线性关系的相关分析 若计量资料变量1,…,变量m服从正态分布,对于它们之间是否存在线性相关关系可以通过相关分析方法,相应的STATA命令为: pwcorr变量名1变 Stata第九章 多因素方差分析命令与输出结果说明本节STATA命令摘要: anova 观察变量 分组变量1 分组变量2… 分组变量m tabulate 分组变量1 分组变量2,summarize(观察变量) 在anova命令中分组变量可以是其它分组变量的乘积表达式,如:分组变量1*分组变量2。 例:治疗缺铁性贫血病 第十章 线性回归和逐步回归命令和输出结果说明本 节STATA 命 令 摘 要: regress 因变量 变 量1 变 量2… 变 量m,beta stepwise 因变量 变 量1 变 量2… 变 量m,ba forw st fe(#) fs(#) test 表 达 式 predict& Stata第八章 单因素生存分析本 节STATA 命 令 摘 要 logrank 生存时间变量 结果变量[,by(分组变量)] 单 因 素 生 存 分 析 在 医 学 研 究 中, 除 了 计 量 资 料 和 计 数 资 料 外, 还 经 常 遇 到 生 存 分 析 的 资 料, 这 种 资 料 不 仅 描 述 所 观 察 对 象 是 否 有 结 果( 死 亡 |
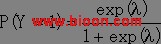


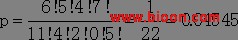





#logistic回归#
105
#Logistic#
78
难得有这么好的网站!
20
#回归分析#
68
#GIST#
68