两总体的wilcoxon秩检验与Kruskal-walls检验的关系
2012-04-13 陈辉蓉 数理医药学杂志
在统计检验中,对两总体的位置参数进行检验,若已知总体的分布,则可用传统的参数检验法;当总体的分布未知时,可用非参数检验法。如wilcoxon检验、Kruakal-wallis检验,但这两者之间有什么关系呢?又有什么区别呢?本文对此进行了探讨。 1 两种检验之间的一致 设Xil…Xini分别来自分布F(x-θi)的独立大样本,i=1,2,记,且n2≤n1,将两样本混合编秩,记Rij为Xij在合
在统计检验中,对两总体的位置参数进行检验,若已知总体的分布,则可用传统的参数检验法;当总体的分布未知时,可用非参数检验法。如wilcoxon检验、Kruakal-wallis检验,但这两者之间有什么关系呢?又有什么区别呢?本文对此进行了探讨。
1 两种检验之间的一致
设Xil…Xini分别来自分布F(x-θi)的独立大样本,i=1,2,记 ,且n2≤n1,将两样本混合编秩,记Rij为Xij在合样本中的秩。
,且n2≤n1,将两样本混合编秩,记Rij为Xij在合样本中的秩。
1.1 当两样本中无结时,Wilcoxon检验的统计量为: (1)
(1)
其中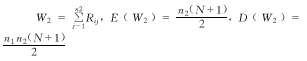 而kruskal-wallis检验统计量为:
而kruskal-wallis检验统计量为: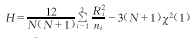 (2)
(2)
其中 即
即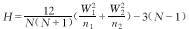 (3)
(3)
由于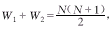 ,则
,则![]() 于是
于是 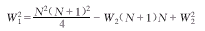 (4)
(4)
将(4)代入(3)可得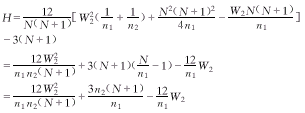 将(1)平方后得
将(1)平方后得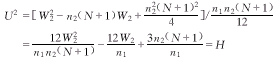 所以, U2=H。
所以, U2=H。
1.2 当两样本中有g个结时,Wilcoxon统计量为:
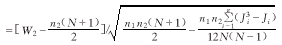 (5)
(5)
其中Ji为第i个结的长度。
而 (6)
(6)
同理可得: Hc=U2c。
对于检验H0∶θ1=θ2,H1∶θ1≠θ2,U统计量的拒绝域为 ,H统计量的拒绝域为
,H统计量的拒绝域为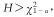 ,由于
,由于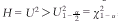 ,故两检验是一致的。
,故两检验是一致的。
例如[1],为了比较甲、乙两种香烟的尼古丁含量(mg),对甲种香烟作了6次测定,对乙种香烟作了8次测定,数据见表1。
表1 甲、乙两种香烟尼古丁含量
| 香烟品种 | 尼古丁含量(mg) |
| 甲 | 25 28 23 26 29 22 |
| 乙 | 28 31 30 32 21 27 24 20 |
于是U2c=0.3364=Hc,两测量结果一致(差异是由于计算引起的)。
2 两检验的区别
Wiloxon检验是有方向性的。因为对于单侧检验
H0∶θ1=θ2,H1∶θ1>θ2(或θ1<θ2)
拒绝域为U<-U1-α(或U>U1-α),而kruskal-wallis检验无法反映这种方向性[2]。
3 结果分析
3.1 由上面的讨论可知,对于两总体位置参数的双侧检验Wilcoxon检验和kruskal-wallis检验是一致的。
3.2 Wilcoxon检验是有方向的,而kruskal-wallis检验是无方向的。
3.3 当作单侧检验时用Wilcoxon检验。
参考文献
1,周怀梧主编.医药应用概率统计,百家出版社,1990,2.
2,吴喜之,王兆军著.非参数检验.等等教育出版社,1996,9.
本网站所有内容来源注明为“梅斯医学”或“MedSci原创”的文字、图片和音视频资料,版权均属于梅斯医学所有。非经授权,任何媒体、网站或个人不得转载,授权转载时须注明来源为“梅斯医学”。其它来源的文章系转载文章,或“梅斯号”自媒体发布的文章,仅系出于传递更多信息之目的,本站仅负责审核内容合规,其内容不代表本站立场,本站不负责内容的准确性和版权。如果存在侵权、或不希望被转载的媒体或个人可与我们联系,我们将立即进行删除处理。
在此留言







#ALL#
60