SAS第七课:方差分析与协方差分析
2012-04-17 生物谷 生物谷
方差分析和协方差分析在SAS系统中由SAS/STAT模块来完成,其中我们常用的有ANOVA过程和GLM过程。前者运算速度较快,但功能较为有限;后者运算速度较慢,但功能强大,我们做协方差分析时就要用到GLM过程。本章将首先介绍方差分析所用数据集的建立技巧,然后重点介绍这两个程序步。 其实,这里的速度快慢只是相对而言,SAS的处理速度是首屈一指的。举个例子,这个暑假我做了一个有66
方差分析和协方差分析在SAS系统中由SAS/STAT模块来完成,其中我们常用的有ANOVA过程和GLM过程。前者运算速度较快,但功能较为有限;后者运算速度较慢,但功能强大,我们做协方差分析时就要用到GLM过程。本章将首先介绍方差分析所用数据集的建立技巧,然后重点介绍这两个程序步。
其实,这里的速度快慢只是相对而言,SAS的处理速度是首屈一指的。举个例子,这个暑假我做了一个有6600条记录的,7因素的,交叉设计的方差分析(是不是已经有人喊头痛了?),我先是用SPSS FOR WIN95 7.5来做,运行了大约10分钟才出结果。我又换用SAS FOR WIN95 6.12来做,结果用了――2.47秒!§
7.1 方差分析数据集的建立技巧7.1.1
方差分析的数据集格式统计分析所用的数据格式和我们在分析整理资料时所用的格式是不同的。一般来说,数据集中应至少有一个结果变量,用于记录不同处理因素水平下观察值的大小;至少有一个处理因素变量,用于记录处理因素的类型及其水平数。以单因素方差分析为例,就应有一个结果变量和一个处理因素变量;而两因素的方差分析应有一个结果变量和两个处理因素变量。
例
7.1 某职业病防治院对31名石棉矿工中的石棉肺患者、可疑患者及非患者进行了用力肺活量测定,请给出数据集的结构(卫统p44 例5.1)。解:数据集中应有两个变量,
x和group。x记录肺活量的大小;group取值为1、2或3,分别代表石棉肺患者、可疑患者及非患者。例
7.2 某厂医务室测定了10名氟作业工人工前、工中及工后4小时的尿氟浓度,请给出数据集的结构(卫统p46 例5.2)。解:数据集中应有三个变量,
x、group和worker。x记录尿氟浓度;group取值为1、2或3,分别代表工前、工中及工后;worker取值为1到10,分别代表10名工人。7.1.2
方差分析数据集的建立技巧可见方差分析的数据集其变量取值有一定的规律,因此可以利用循环语句和判断语句来简化输入。
例
7.3 请建立例6.1的数据集。解:我们可以一个一个的输入变量
group的值,但这里给出一种更酷的建立方法。|
libname a 'c:\user'; | |
|
data a.wtli5_1; | |
|
group=1; | |
|
if _n_>11 then |
此处的_n_为SAS系统变量,表明读入的数据为第几条记录,由于石棉肺患者只有11人,因此第12条记录只能是可疑患者的记录,同理,从第20条记录开始的只能是非患者的记录。这里利用判断语句来完成从_n_到group的转换。 |
|
if _n_>20 then group=3; | |
|
else group=2; | |
|
; | |
|
input value @@; | |
|
cards; | |
|
1.8 1.4 1.5 2.1 ... ... 3.3 3.5 | |
|
; | |
|
proc print; | |
|
run; | |
例
7.4 请建立例7.2的数据集。解:此例中数据较有规律,各组的例数均相等,这可正是循环语句大显身手的时候。
|
libname a 'c:\user'; | |
|
data a.wtli5_2; | |
|
do group=1 to 3; |
这里的SAS语句非常类似于Foxbase语句,两个循环分别控制了group和worker的取值,这在输入数据时是常见的一种技巧。 |
|
do worker=1 to 10; | |
|
input value @@; | |
|
output; |
两个变量只是循环变量,因此要用output语句写入数据集中。 |
|
end; | |
|
end; | |
|
cards; | |
|
90.53 88.43 47.37 ... |
请注意x变量和处理因素变量的对应关系,不要改变数据块的次序,否则建立的数据集是错的。 |
|
; | |
|
proc print; | |
|
run; | |
§
7.2 引 例例
7.5 请回答在例7.1中三组石棉矿工的用力肺活量有无差别?解:由于是三组做比较,因此要用方差分析法。在建立数据集后可用
ANOVA过程或GLM过程进行分析,同时给出选项进行各组均数的两两比较(此处用SNK法),两过程的输出格式基本一致。对于单因素的方差分析,在比较之前一般要考虑方差齐性的问题。这里可以用GLM过程中的HOVTEST选项实现,实际上这也是在SAS中做方差齐性检验的唯一途径。①
设定数据库环境:LIBNAME A
'C:\USER';②
数据步,建立数据集(略):③
ANOVA或GLM过程,进行方差分析并同时做两两比较(SNK法):|
PROC ANOVA DATA=A.WTLI5_1; |
PROC GLM DATA=A.WTLI5_1; |
|
CLASS GROUP; |
CLASS GROUP; |
|
MODEL VALUE=GROUP; |
MODEL VALUE=GROUP /SS1; |
|
MEAN GROUP /SNK; |
MEAN GROUP /SNK HOVTEST; |
|
RUN; |
RUN; |
![]()
§
7.3 ANOVA过程ANOVA
过程是SAS系统中用于方差分析的几个程序步之一,它适用于平衡的数据。这意味着如果按所分析的变量将观测值分类,则每个格子内的观测值数目应相同。如果数据不满足这一要求,则ANOVA过程的分析结果并不可靠,分析者应改用GLM过程来处理数据。7.3.1
语法格式|
PROC ANOVA [DATA= <数据集名> |
|
|
MANOVA |
按多元分析的要求略去有任一缺失值的记录 |
|
OUTSTAT= <数据集名>] ; |
指定统计结果输出的数据集名 |
|
CLASS <处理因素名列>; |
必需,指定要分析的处理因素 |
|
MODEL <应变量名=处理因素名列> / [选项]; |
必需,给出分析用的方差分析模型 |
|
MEANS <变量名列> / [选项] ; |
指定要两两比较的因素及比较方法 |
|
BY <变量名列>; |
|
|
FREQ <变量名>; |
|
|
MANOVA H= 效应 E= 效应 M= 公式...; |
指定多元方差分析的选项 |
7.3.2
语法说明Means
语句的选项主要用来指定两两比较的方法和检验水准,主要有:- 两两比较方法
7.3.3
结果解释这里以例
7.2的数据为例,ANOVA过程的输出结果分两大部分,第一部分是分析变量的列表描述,第二部分是统计结果,先是所用方差分析模型的检验,然后是各个处理因素和交互作用的检验结果,最后则是两两比较的结果。 Analysis of Variance Procedure 方差分析过程
Class Level Information 处理因素取值情况Class Levels Values 处理因素变量名 取值数 具体值 GROUP 3 1 2 3 WORKER 10 1 2 3 4 5 6 7 8 9 10
Number of observations in data set = 30 样本大小为30
--------------以下为方差分析的统计结果部分,首先是对方差分析所用模型的检验-------------
Analysis of Variance Procedure
Dependent Variable: VALUE 应变量名为VALUE
Source DF Sum of Squares Mean Square F Value Pr > F 变异来源 自由度 SS MS F p值
Model 11 47895.87728667 4354.17066242 4.51 0.0024 Error 18 17365.56086000 964.75338111 Corrected Total 29 65261.43814667
R-Square C.V. Root MSE 应变量名 Mean
所用模型的决定系数 变异系数 剩余标准差 应变量均数
0.733908 28.27501 31.06047941 109.85133333-----------统计结果的第二部分,对各个具体处理因素及其交互作用的检验----------
Dependent Variable: VALUE
Source DF Anova SS Mean Square F Value Pr > F 变异来源 自由度 SS MS F p值
GROUP 2 8182.89340667 4091.44670333 4.24 0.0310 WORKER 9 39712.98388000 4412.55376444 4.57 0.0030
---------统计结果的第三部分,对GROUP变量做两两比较,只有MEAN语句中指定了才会出现------
Analysis of Variance Procedure
Student-Newman-Keuls test for variable: VALUE
注意这里我们用SNK法做例子,其余比较方法的输出结果与之类似
NOTE: This test controls the type I experimentwise error rate under the
complete null hypothesis but not under partial null hypotheses. Alpha= 0.05 df= 18 MSE= 964.7534
α水准为0.05,自由度为18,MS误差为964.7534 Number of Means 2 3
Critical Range 29.183219 35.451257
SNK法两两比较时的界值,两均数之差大于该界值时则两组有统计学差异Means with the same letter are not significantly different.
SNK Grouping Mean N group(处理因素变量名)
A 126.59 10 2
A
B A 115.59 10 3
B
B 87.38 10 1
检验的分组结果 各组均数 例数 组别
注:为了便于理解,SAS将两两比较的结果直接用英文字母的形式标示出来。两两比较结果的最右侧是处理因素变量的取值,最左侧标以字母A、B、C等等,用以表示该处理组和其它组有无差异。如果两组有相同的字母(如2、3两组),则两者之间无差异;而如果两组间只有不同的字母,则表示两组间的差异有统计学意义。可以看出此次比较的结果为:1组和2组有区别,其余均两两无区别。
7.3.4
应用实例例
7.6 现测定了某湖湖水不同季节氯化物的含量,问不同季节氯化物含量有无区别(卫统p226 2.6题)?解:
|
data a.wt2_6; | |
|
do season=1 to 4; | |
|
input x @@; | |
|
output; | |
|
end; | |
|
cards; | |
|
22.6 19.1 ... 19.6 14.8 |
注意输入次序 |
|
; | |
|
proc anova data=a.wt2_6; | |
|
class season; | |
|
model x=season; | |
|
mean season/snk; | |
|
run; | |
![]()
你们到底要我怎么写才好
...§
7.4 GLM过程GLM
过程即广义线形模型(General Liner Model)过程,它使用最小二乘法对数据拟合广义线形模型。GLM过程中可以进行回归分析、方差分析、协方差分析、剂量――反应模型分析、多元方差分析和偏相关分析等等,其功能之强大可见一斑。![]()
7.4.1
语法格式非常走运,在我们所用到的范围里,
GLM过程的语法结构和ANOVA过程完全相同,这可大大的方便了我们的学习。这里我们只解释协方差分析的做法:由于协变量并非我们研究的处理因素,因此在CLASS语句中可不能有它的位置;但是,另一方面协变量要影响结果变量的取值,因此必须在模型中引入,怎么办?只要在MODEL语句中将其写入即可(写在分析变量的首位)。瞧,就这么简单!7.4.2
结果解释这次我们仍然很走运,
GLM过程的结果和ANOVA过程是雷同的――注意是雷同而不是相同。在处理因素、协变量及交互作用的检验结果部分,GLM过程会给出两种结果(Ⅰ类和Ⅲ类结果)。在我们用到的范围里,两种结果是完全相同的,所以用哪一种都可以。7.4.3
应用实例例
7.7 今用A、B两药治疗12名贫血病人,测得治疗一个月时的红细胞增加数(百万/mm3),问两药的治疗效果如何,两药同时使用的效果如何(医统第二版P92 例5.5)?解:该实验的设计为析因设计,在分析时要将交互作用考虑在内。程序如下:
|
data a.ytli5_5; | |
|
do b=1 to 0 by -1; | |
|
do a=1 to 0 by -1; | |
|
do tmpvar=1 to 3; |
tmpvar为临时变量,使一个格子里有3个观测值 |
|
input x@@; | |
|
output; | |
|
end; | |
|
end; | |
|
end; | |
|
drop tmpvar; |
删除临时变量tmpvar |
|
cards; | |
|
2.1 2.2 2.0 0.9 1.1 1.0 | |
|
1.3 1.2 1.1 0.8 0.9 0.7 | |
|
; | |
|
proc glm data=a.ytli3_4; | |
|
class a b; | |
|
model x=a b a*b; |
a*b表示a、b的交互作用 |
|
run; | |
例
7.8 请给出《医学统计学》第一版108页例6.1的分析程序。解:协方差分析的关键步骤是分析资料是否满足协方差分析的应用条件,程序如下:
|
data a.ytli6_1; | |
|
group=1; | |
|
if _n_>13 then group=2; | |
|
input y x@@; | |
|
cards; | |
|
3.7 15.73 2.35 11.7 ... | |
|
... 21.43 9.62 1.3 6.89 | |
|
; | |
|
proc gplot; |
做散点图,比较两组的相关趋势 |
|
plot y*x=group ; |
按group变量分组绘图 |
|
symbol1 i=rl v=star; |
在散点图上加回归线 |
|
symbol2 i=rl v=plus; |
|
|
proc reg; |
做x、y的回归分析 |
|
model y=x; | |
|
by group; | |
|
proc glm data=a.ytli6_1; | |
|
class group; | |
|
model y= x group; |
x为协变量 |
|
run; | |
(原著:张文彤)
本网站所有内容来源注明为“梅斯医学”或“MedSci原创”的文字、图片和音视频资料,版权均属于梅斯医学所有。非经授权,任何媒体、网站或个人不得转载,授权转载时须注明来源为“梅斯医学”。其它来源的文章系转载文章,或“梅斯号”自媒体发布的文章,仅系出于传递更多信息之目的,本站仅负责审核内容合规,其内容不代表本站立场,本站不负责内容的准确性和版权。如果存在侵权、或不希望被转载的媒体或个人可与我们联系,我们将立即进行删除处理。
在此留言






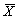




#SAS#
75
#协方差#
0