SAS第八课:直线回归、直线相关与Logistic回归(上)
2012-04-17 生物谷 生物谷
直线回归与相关是联系非常紧密的两种统计分析方法,事实上SAS用于回归分析的程序步REG也可提供相关分析的结果,但进一步的深入分析仍应采用相应的程序步--CORR才能实现。本章前三节主要介绍两个常用的用于直线回归和相关分析的程序步――REG过程和CORR过程。后两节则介绍多元线性回归和Logistic回归的方法和所用的过程。 §8.1 引 例 例8.1 今测定20名糖尿病人血糖
直线回归与相关是联系非常紧密的两种统计分析方法,事实上SAS用于回归分析的程序步REG也可提供相关分析的结果,但进一步的深入分析仍应采用相应的程序步--CORR才能实现。本章前三节主要介绍两个常用的用于直线回归和相关分析的程序步――REG过程和CORR过程。后两节则介绍多元线性回归和Logistic回归的方法和所用的过程。
§8.1 引 例
例
8.1 今测定20名糖尿病人血糖水平(mmol/L)与胰岛素水平(mU/L),试以血糖为应变量Y,胰岛素为自变量X建立直线回归方程,并求两者的相关系数(医统第二版P104例6.1)。解:显然,在建立数据集时应指定血糖与胰岛素两个变量。再调用
GPLOT过程绘制散点图观察有无直线趋势,然后调用REG过程求出直线回归方程,最后调用CORR过程求出相关系数。①
设定数据库环境:LIBNAME A
’C:\USER’;②
数据步,建立数据集:|
DATA A.YTLI7_1; |
|
INPUT Y X @@; |
|
CARDS; |
|
12.21 15.2 14.54 16.7 12.27 11.9 12.04 14.0 7.88 19.8 11.10 16.2 |
|
10.43 17.0 13.32 10.3 19.59 5.9 9.05 18.7 6.44 25.1 9.49 16.4 |
|
10.16 22.0 8.38 23.1 8.49 23.2 7.71 25.0 11.38 16.8 10.82 11.2 |
|
12.49 13.7 9.21 24.4 |
|
; |
|
RUN; |
③
做散点图,估计两变量有无直线趋势:|
PROC GPLOT DATA=A.YTLI7_1; |
|
PLOT Y*X; |
|
RUN; |
④
REG过程,进行直线回归分析:|
PROC REG DATA=A.YTLI7_1; |
|
MODEL Y = X; |
|
RUN; |
⑤
CORR过程,进行相关分析:|
PROC CORR DATA=A.YTLI7_1; |
|
VAR X Y ; |
|
RUN; |
§8.2 REG过程
SAS/STAT
模块提供了近十个用于回归分析的过程,其中REG过程是进行一般线性回归分析最常用的过程,该过程采用最小二乘法拟合线性模型,可产生有关数据的一些描述统计量、参数估计和假设检验以及散点图,输出预测值、残差、学生化残差、可信限等,并可将这些结果输出到一个新的SAS数据集中。8.2.1 语法格式
REG
过程的语法格式如下:|
PROC REG [DATA=<数据集名> [选项] ] ; |
|
MODEL 应变量名=自变量名列/ [选项] ;[1] |
|
[VAR 变量名列;[2] |
|
FREQ 变量名; |
|
WEIGHT 变量名; |
|
BY 变量名列; |
|
OUTPUT |
|
PLOT <纵坐标变量*横坐标变量[=绘图符号]...> / [选项];[3]] |
8.2.2 语法说明
程序中全部语句中只有第一行和
MODEL语句是必需的,其他都可以省略。【过程选项】
- OUTEST= 数据集名 指定统计量和参数估计输出的新数据集名。
- NOPRINT 禁止统计结果在OUTPUT视窗中输出。
- SIMPLE 输出REG过程中所用的每个变量的基本统计量。
- CORR 输出MODEL语句或VAR语句中所列变量的相关矩阵。
- ALL 等价于MODEL语句加上全部选项,即输出该语句所有选项分析结果。
【MODEL语句】
MODEL
语句定义模型中的因变量、自变量、模型选项及结果输出选项。语句中的变量只能是数据集中的变量,任何形式的变换都必须先产生一个新变量,然后用于分析。如X1的二次项,不能在模型中直接指定X1*X1,而要产生另一个新变量代表X1*X1,方可引入模型。MODEL
语句中常用的选项有:- NOINT 在模型中不拟合常数项。
- STB 输出标准化回归系数。
- CLI 输出个体预测值
- CLM 输出因变量期望值(均值)的95%可信区间上下限。
- R 输出个体预测值、残差及其标准误。
- P 输出实际值Yi、预测值
【关键字】
REG
过程中OUTPUT语句的用法和UNIVARIATE过程中的用法相同,只是会用到另一些关键字。关键字用来定义需要输出到新数据集中的统计量,常用的关键字及其含义有:|
PREDICTED |
因变量预测值(简写为P) |
RESIDUAL |
残差(简写为R) |
|
L95M、U95M |
均数95%可信区间上下限 |
L95、U95 |
个体预测值95%可信区间上下限 |
|
STDP |
期望值的标准误 |
STDR |
残差的标准误 |
|
STDI |
预测值的标准误 |
STUDENT |
学生化残差(即残差与标准误之比) |
【
PLOT语句】PLOT
语句用于输出变量间的散点图,其用法和GPLOT过程中的PLOT语句非常相似。PLOT语句定义的两变量可为MODEL语句或VAR语句中定义的任何变量。SYMBOL选项可定义散点图中点的标记,如SYMBOL=’*’,则每个点以“*”表示。8.2.3 结果解释
REG
过程的默认输出结果和方差分析输出结果相似,这是因为它们所用的统计模型相同。刚才的例4.1输出结果如下:Model: MODEL1 第一个模型 Dependent Variable: Y 应变量名为Y
----以下是REG过程给出的直线回归方程是否有统计学意义的检验结果,使用的检验方法为方差分析---
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Prob>F
变异来源 自由度 离均差平方和 均方 F值 P值
回归变异 Model 1 114.70324 114.70324 43.060 0.0001
误 差 Error 18 47.94816 2.66379
总变异 C Total 19 162.65140 误差的均方根 Root MSE 1.63211 R-square 0.7052 确定系数R2
 Dep Mean 10.85000 Adj R-sq 0.6888 调整的R2
Y的变异系数 C.V. 15.04250
Dep Mean 10.85000 Adj R-sq 0.6888 调整的R2
Y的变异系数 C.V. 15.04250
--------以下是参数估计及其假设检验结果,采用的是t检验--------
Parameter Estimates
Parameter Standard T for H0:
Variable DF Estimate Error Parameter=0 Prob > |T|
变量名 自由度 参数估计值 估计值的标准误Sb t值 P值
截距 INTERCEP 1 18.796143 1.26472741 14.862 0.0001
X 1 -0.458520 0.06987466 -6.562 0.0001
如果在
MODEL语句中使用CLI、CLM选项,则系统输出因变量均值以及个体预测值的95%可信区间上下限,输出如下: Dep Var Predict Std Err Lower95% Upper95% Lower95% Upper95%
Obs Y Value Predict Mean Mean Predict Predict
1 12.2100 11.8266 0.394 10.9986 12.6547 8.2991 15.3541
记录号 Y的实测值 预测值 预测值的标准误  可信区间的上下限 个体预测值可信区间的上下限
Y
可信区间的上下限 个体预测值可信区间的上下限
Y 
 (
( ) (
) ( )
) Obs Residual
记录号 残差
1 0.3834Sum of Residuals 0 残差和 Sum of Squared Residuals 47.9482 残差平方和 Predicted Resid SS (Press) 66.8422 预测残差平方和
§8.3 CORR过程
CORR
过程计算变量间的相关系数,包括Pearson积矩相关系数、Spearman等级相关系数等,同时也可给出一些单变量描述统计结果。8.3.1 语法格式
CORR
过程的语法格式如下:|
PROC CORR [选项] ; |
|
[VAR 变量名列 ;[1] |
|
WITH 变量名列;[2] |
|
WEIGHT 变量名; |
|
FREQ 变量名; |
|
BY 变量名列;] |
8.3.2 语法说明
除了
PROC语句为必需,其他语句都是可选的,如果省略所有的可选语句,则对所有变量作相关分析。【过程选项】
- 数据集选项
- DATA=
-
相关类型选项
- PEARSON
-
其它选项
-
NOMISS
NOPRINT
NOSIMPLE
【
VAR语句和WITH语句】VAR
语句给出希望计算相关的变量名。若省略该语句,则CORR过程计算指定数据集中所有数值变量间各种组合的相关系数。WITH
语句必须和VAR语句一同使用。如果我们要得到特定变量组合的相关系数,则可在VAR语句中列出相关矩阵上部出现的变量,在WITH语句中列出相关矩阵左侧出现的变量。如有程序步如下:PROC CORR
;VAR A B
;WITH X Y Z
; 则产生下列组合的相关系数矩阵:|
A |
B | |
|
X |
rXA |
rXB |
|
Y |
rYA |
rYB |
|
Z |
rZA |
rZB |
8.3.3 结果解释
CORR
过程的默认输出结果主要包括各个变量的简单统计描述和一个相关系数矩阵。例8.1的CORR过程的具体输出如下:Correlation Analysis
2 'VAR' Variables: X Y 相关阵中的变量有X、Y
Simple Statistics 简单统计描述
Variable N Mean Std Dev Sum Minimum Maximum 变量名 例数 均数 标准差 总和 最小值 最大值 X 20 17.330000 5.358623 346.600000 5.900000 25.100000 Y 20 10.850000 2.925850 217.000000 6.440000 19.590000
Pearson Correlation Coefficients / Prob > |R| under Ho: Rho=0 / N = 20
-------矩阵第一列为PEARSON相关系数,第二列为相应的P值。并且该样本的例数为20-----
X Y X 1.00000 -0.83977
0.0 0.0001 Y -0.83977 1.00000
0.0001 0.0
本例X与Y的相关系数达到-0.83977,检验相关系数检验的P值为0.0001,按α=0.05水准,拒绝H0,接受H1,相关系数检验由统计学意义,血糖和胰岛素之间由直线相关关系。
8.3.4 应用实例
例
8.2 下表给出了12名不同年龄(岁,X)妇女的收缩压测量值(mmHg,Y),试进行回归分析。|
妇女 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
年龄 |
56 |
42 |
72 |
36 |
63 |
47 |
55 |
49 |
38 |
42 |
68 |
60 |
|
血压 |
147 |
125 |
160 |
118 |
149 |
128 |
150 |
145 |
115 |
140 |
152 |
155 |
- 制作散点图;
(2)
建立由X预报(3)
对回归方程及回归系数b进行假设检验;(4)
绘制(5)
建立单个Y值的预报方程;(6)
计算积矩相关系数,并进行假设检验。解:程序如下:
|
data a.yt4_10; |
|
input x y @@; |
|
cards; |
|
56 147 ... ... 60 155 |
|
; |
|
proc gplot; |
|
plot y*x y*x/overlay; |
|
symbol1 v=star c=pink ; |
|
symbol2 i=rlcli c=blue ; |
|
proc corr; |
|
var x y; |
|
proc reg; |
|
model y = x / cli clm; |
|
run; |
GPLOT
过程绘制高分辨率的图形,在PLOT语句中作了两层图,用OVERLAY选项让它们在同一坐标系中绘制,第一层图绘制散点图,用星号表示散点,颜色为粉红色;第二层图绘制回归直线和个体预测值95%可信区间,颜色为兰色。用了两个SYMBOL语句分别控制这两层图的输出效果。该过程的输出在GRAPH窗口。 其他两个过程的输出同前类似,不再赘述。
(原著:李晓松 田晓燕)
本网站所有内容来源注明为“梅斯医学”或“MedSci原创”的文字、图片和音视频资料,版权均属于梅斯医学所有。非经授权,任何媒体、网站或个人不得转载,授权转载时须注明来源为“梅斯医学”。其它来源的文章系转载文章,或“梅斯号”自媒体发布的文章,仅系出于传递更多信息之目的,本站仅负责审核内容合规,其内容不代表本站立场,本站不负责内容的准确性和版权。如果存在侵权、或不希望被转载的媒体或个人可与我们联系,我们将立即进行删除处理。
在此留言

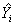








#SAS#
70
#logistic回归#
67
#Logistic#
72
#GIST#
54